Scratch

Aquí dejamos el link de los retos de nuestra cuenta de scratch:

-Reto 1:
https://scratch.mit.edu/projects/153987830/

-Reto 2:
https://scratch.mit.edu/projects/156095864/

-Reto 3:
https://scratch.mit.edu/projects/156098807/

-Reto 4:
https://scratch.mit.edu/projects/156100757/

-Reto 5:
https://scratch.mit.edu/projects/156103487/

-Reto 6:
https://scratch.mit.edu/projects/156108920/

-Reto 7:
https://scratch.mit.edu/projects/156232350/

-Reto 8:
https://scratch.mit.edu/projects/156242163/

-Reto 9:
https://scratch.mit.edu/projects/156386421/

-Reto 10:


-Reto 11:
https://scratch.mit.edu/projects/156500707/

-Reto 12:
https://scratch.mit.edu/projects/156491510/

Trabajo funciones

MATEMÁTICAS: ACTIVIDADES SOBRE FUNCIONES

1ª PARTE: Conceptos básicos:

1. ¿Cómo puedes expresar la relación entre dos magnitudes como, por ejemplo, la masa y el volumen de un cuerpo? 

La propiedad que mide la pesadez de una sustancia es la densidad. Cuanto mayor sea, más pesado parecerá. La densidad es la masa de un cuerpo entre el volumen que ocupa. Aunque toda la materia posee masa y volumen, la misma masa de sustancias diferentes ocupan distintos volúmenes, así notamos como algo es pesado y algo es ligero.

2. ¿Qué es una función? ¿De qué formas pueden expresarse las relaciones entre magnitudes? Pon ejemplos de funciones de la vida cotidiana; puedes buscar en revistas, periódicos, etc. En las figuras siguientes tienes 3 ejemplos: 

• Una función es una correspondencia numérica en la que a cada elemento del conjunto inicial se le asigna un único elemento denominado imagen del conjunto final.

• La relación entre magnitudes  se puede expresar mediante el lenguaje en un texto, tablas, gráficas y ecuaciones o expresiones algebraicas.

•  Magnitudes directamente proporcionales: Dos magnitudes son directamente proporcionales, si al cambiar el valor de la magnitud independiente, los valores de la magnitud dependiente cambian en la misma proporción.
• Ejemplos:
• Cuanta más luz gaste más pago en la factura de la luz.
• Cuantas más personas invitadas a comer más comida debo comprar.

• Magnitudes inversamente proporcionales: Dos magnitudes son inversamente proporcionales, cuando el valor de la magnitud independiente es creciente, el valor de la magnitud dependiente es decreciente en la misma magnitud.
• Ejemplos:
• Para llenar un recipiente cuantas más mangueras abra menos tiempo tarda.
• Cuanto más suben los precios menos cosas puedo comprarcon el mismo dinero.

3. ¿Qué es la tasa de variación de una función? ¿Qué valores toma para las funciones crecientes y decrecientes? Puedes utilizar ejemplos gráficos para responder.

La tasa de variación de una función es el incremento  o disminución que experimenta la función, al pasar la variable independiente de una valor a otro y esta variación nos da un número.

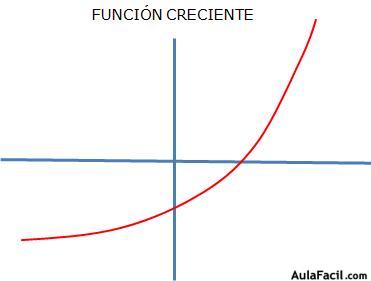Sí este número es > 0 decimos que la función es creciente

 Sí por el contrario, es < 0 decimos que la función es decreciente.

4. Utilizando la representación gráfica de una o varias funciones, explica las diferencias entre máximos y mínimos absolutos y relativos.

El máximo y mínimo absoluto en una función, el máximo es cuando la ordenada es mayor o igual que en cualquier otro punto del dominio de la función. Por otro lado, la función tiene su mínimo absoluto si la ordenada es menor o igual a cualquier otro punto de la función.

La función tiene un máximo y mínimo relativo  el máximo relativo en el punto  a(-1,2), si f(a) es mayor o igual que los puntos próximos al punto a. En cambio, La función tiene un mínimo relativo en el punto b (1,-2), si f(b) es menor o igual que los puntos próximos al punto b.

5. Representa gráficamente dos ejemplos de funciones simétricas respecto al eje de ordenadas (eje y) y respecto al origen (0,0). Explica en qué consiste cada tipo de simetría.

    Se dice que una función es par f(x) = f(-x) ; en el caso de que f(x) = -f(-x) se dice que la función es impar.

      En la imagen del medio observamos que es simétrica al eje y ya que en los dos lados son iguales.

 6. Representa gráficamente una función periódica indicando por qué se denomina de esa forma.

Las funciones periódicas son aquellas en las que tienen ondas que muestran periodicidad respecto al tiempo, es decir, describen ciclos repetitivo

7. Pon dos ejemplos, uno de función continua y otro de función discontinua. ¿Cuál es la diferencia entre ambas? 

Una función continua es un valor de la variable independiente cuyas imágenes se aproximan a la imagen, es decir, se pueden unir con una recta. En cambio, las imágenes de las funciones discontinuas no son próximas a la imagen, hay un espacio.

Función discontinua y función discontinua

8. Investiga: ¿Cuál es el origen del término función?

La palabra función viene del latín functio, ‘Ejecución, ejercicio de alguna facultad, función,

cumplimiento de un deber’. Éste, del verbo fungi, ‘cumplir, desempeñar una función,

satisfacer, pagar, cumplir, emplear, gozar de’.

2ª PARTE: Estudio y representación de funciones

Para realizar las actividades propuestas en esta parte puedes utilizar alguno de los programas que te recomiendo: Fooplot, Symbolab, Geogebra, Funciones para Windows, Derive, etc. 

9. Representa gráficamente las funciones que se proponen indicando sus propiedades. Elabora una tabla resumen con todas las gráficas obtenidas. 

a) Función lineal creciente

Una función f es creciente si al aumentar la variable independiente x, aumenta la variable dependiente y. 

La función es estrictamente creciente en todo su dominio si para cualquier par de puntos x1 y x2 tales que x1<x2, se cumple que f(x1) < f(x2).

b) Función lineal decreciente

Una función f es decreciente si al aumentar la variable independiente x, disminuye la variable dependiente y. Es decir, la función f es decreciente si para cualquier par de puntos x1 y x2 del dominio tales que x1<x2, se cumple que f(x1) ≥ f(x2). Su pendiente m<0.

La función es estrictamente decreciente en todo su dominio si para cualquier par de puntos x1 y x2 tales que x1<x2, se cumple que f(x1) > f(x2).

c) Función lineal constante

La función constante es del tipo: y = n

El criterio viene dado por un número real.

Su pendiente m=0.

La gráfica es una recta horizontal paralela a al eje de abscisas.

En resumen:

d) Rectas paralelas

Dos rectas paralelas tienen la misma pendiente.

e) Función cuadrática cóncava

Si  a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba.

f) Función cuadrática convexa

Si  a < 0 (negativo) la parábola es convexa o con puntas hacia abajo

Además, cuanto mayor sea |a| (el valor absoluto de a), más cerrada es la parábola.

 g) Investiga sobre la representación gráfica de otras funciones

La función exponencial o hipérbola es del tipo:  Siendo a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llama función exponencial de base a y exponente x.

Ejemplos:  f(x)=2^x

 

X	Y= 2X
-3	1/8
-2	¼
-1	½
0	1
1	2
2	4
3	8

 

f(x)=(1/2)^x

 

X	Y= (½)x
-3	8
-2	4
-1	2
0	1
1	1/2
2	¼
3	1/8

 

PROPIEDADES DE LA FUNCIÓN EXPONENCIAL

Dominio: R 

Recorrido: R+ 

Es continua.

Los puntos (0, 1) y (1, a) pertenecen a la gráfica.

Es inyectiva a ≠ 1(ninguna imagen tiene más de un original).

Creciente si a > 1.

Decreciente si a < 1.

Las curvas y = ax e y = (1/a) x  son simétricas respecto del eje OY.

12.Utiliza el programa que has elegido para resolver gráficamente el sistema de dos ecuaciones lineales con dos incógnitas siguiente: 

13.Elige un modelo de coche que disponga de motorizaciones diesel y gasolina y realiza un estudio gráfico de la función coste que nos permita averiguar cual es el automóvil más adecuado para nosotros en función del número de kilómetros que recorremos anualmente. (Nota: Necesitas el precio del coche, el del combustible y el consumo combinado)

                                   Modelo Gasolina                                  Modelo Diésel

Precio                                     25000,00                                            8200,00

Consumo 4x100km                      6,9                                                        5,2

Coste/Km                                  0,090735                                            0,0507

Expresión                              Y=25000+0.090735x               Y= 28200+0.0507x

Sale más rentable elegir el modelo Diesel, al fin y al cabo y recorres más km, aunque si lo utilizas poco es mejor el modelo de gasolina. 

14. Interpreta la gráfica del recorrido del Maratón Popular de Madrid

La salida se encuentra a 640m y van subiendo hasta 720m en 5 minutos, después descienden hasta 680m donde se mantiene constante hasta los 10 minutos, a partir de los 10 minutos empieza otra vez a descender hasta situarse por los 640m aproximadamente y se mantiene más menos hasta los 18 minutos, a partir de aquí  suben hasta los 720m en el minuto 25 donde se mantienen hasta minuto 28 que van descendiendo hasta bajar a los 690m en el minuto 30, y siguen descendiendo hasta el minuto 32 a los 650m. A partir de aquí vuelven a subir a los 700m en el minuto 36 y luego van descendiendo hasta mantenerse entre el minuto 37 y 38, para descender bruscamente en el minuto 39 a lo 655m y volver a subir progresivamente a los 680m en el minuto 40 y medio y llegar a la meta en el minuto 42 y medio a 670m.